[LeetCode] 1631. Path With Minimum Effort

출처: leetcode.com/problems/path-with-minimum-effort/

Path With Minimum Effort - LeetCode

문제

당신은 도보 여행을 준비하고 있는 도보 여행자입니다. 당신에게 rows x columns의 크기를 갖는 2차원 배열 heights가 주어집니다. heights[row][col]은 (row, col)칸의 높이가 적혀있습니다. 당신은 왼쪽 상단 (0, 0)에 있고 오른쪽 하단 (rows-1, columns-1)로 가기를 희망합니다. 당신에게는 위, 아래, 왼쪽 또는 오른쪽의 4가지 선택지가 있고, 최소 노력으로 목적지까지 가는 경로를 찾고 싶습니다.

 

경로의 노력는 목적지까지 도착하는 경로에서 연속된 칸 사이의 높이 차 중 최대값 입니다.

 

왼쪽 상단에서 오른쪽 하단까지 이동하는데 필요한 최소 노력을 반환하라.

예제

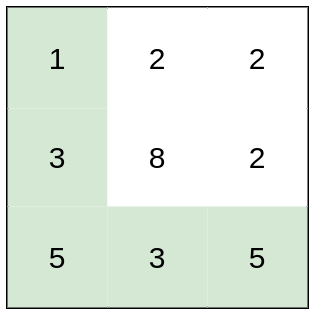
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2

Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.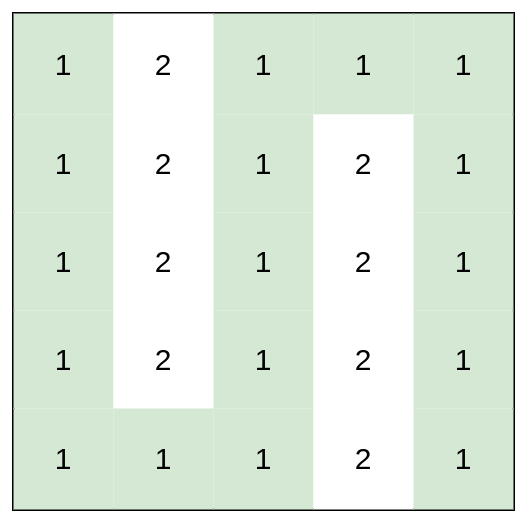

Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0

Explanation: This route does not require any effort.

풀이

이 문제를 효율적으로 풀기 위한 방법에는 다음 두 가지 방식을 생각할 수 있습니다.

 

1. BFS + Greedy => 다익스트라 알고리즘
2. Binary Search + DFS

위의 두 가지 방식 모두 그래프 탐색 알고리즘(BFS, DFS)을 사용합니다. 문제의 상황을 그래프 탐색 문제로 생각할 수 있기 때문입니다. (x, y) 셀을 하나의 노드라고 생각하면, 이 노드는 (x-1, y), (x, y+1), (x+1, y) 그리고 (x, y-1) 노드와 연결된 노드로 생각할 수 있습니다.

 

첫 번째 방식, BFS + Greedy 방식을 살펴보자. BFS를 통해서 목적지까지의 모든 경로를 아래와 같이 탐색할 수 있습니다.

// 큐의 삽입되는 값의 형태는 노드의 좌표 지점 + 방향: [row, col, dir]
const queue = [[0, 0, -1]]
const move = [[-1, 0], [0, 1], [1, 0], [0, -1]];    // move = [up, right, down, left]
while (queue.length) {
    const [cx, cy, cd] = queue.shift();
    for (let dir = 0; dir < 4; i++) {
        // 이전 좌표로 되돌아가는 행위 방지
        if (cd != -1 && cd == (dir+2)%4) { continue; }

          const nx = cx + move[i][0],
              ny = cy + move[i][1];
        // 바운더리 체크
        if (nx < 0 || nx >= rows || ny < 0 || ny >= cols) { continue; }

        queue.push([nx, ny, dir]);
    }
}

이 기본 코드에서 경로의 노력 계산부분을 추가하면 다음의 코드가 됩니다.

// 큐의 삽입되는 값의 형태는 노드의 좌표 지점 + 방향 + 노력: [row, col, dir, effort]
const queue = [[0, 0, -1, 0]]
const move = [[-1, 0], [0, 1], [1, 0], [0, -1]];
while (queue.length) {
    const [cx, cy, cd, ce] = queue.shift();
    for (let dir = 0; dir < 4; i++) {
        if (cd != -1 && cd == (dir+2)%4) { continue; }

          const nx = cx + move[i][0],
              ny = cy + move[i][1];
        if (nx < 0 || nx >= rows || ny < 0 || ny >= cols) { continue; }

        const nc = Math.max(Math.abs(heights[nx] - heights[ny), ce);
        queue.push([nx, ny, dir, nc]);
    }
}

이 상태에서 답을 찾는다면, cx == rows-1 && cy == cols-1를 조건으로 하여 마지막 위치를 찾고 이 때의 노력 값을 기록하여 최소 값을 찾으면 됩니다. 하지만 모든 경로를 다 체크해야 해서 효율적이라고 할 수는 없습니다.

 

다음의 예를 생각해보면, A노드에 최초 진입할때 10의 노력이 드는 경로를 통해서 왔고 이 값을 어딘가 저장했다고 하자. 다른 경로로 다시 A노드에 진입하는 상황이 발생했고, 이때 노력은 15라고 하자. 이 상황에서 A노드의 진입하는게 의미가 있을까. 이전에 알고있는 노력이 더 작기때문에 현재 A노드로의 진입은 불필요한 연산만 추가시킬 뿐 아무런 도움이 되지 않는다. 이러한 부분을 가지치기하여 코드를 개선시켜보면 다음과 같습니다.

// 노드에 도착하는데 필요한 노력을 저장하는 배열 선언
const efforts = new Array(rows).fill(0).map(val => new Array(cols).fill(Infinity));
effort[0][0] = 0;

const queue = [[0, 0, -1, 0]]
const move = [[-1, 0], [0, 1], [1, 0], [0, -1]];
while (queue.length) {
    const [cx, cy, cd, ce] = queue.shift();
    for (let dir = 0; dir < 4; i++) {
        if (cd != -1 && cd == (dir+2)%4) { continue; }

          const nx = cx + move[i][0],
              ny = cy + move[i][1];
        if (nx < 0 || nx >= rows || ny < 0 || ny >= cols) { continue; }

        const nc = Math.max(Math.abs(heights[nx] - heights[ny), ce);
        // 이전에 알고있는 노력과 비교하여 가지치기 수행
        if (efforts[nx][ny] > nc) {
            efforts[nx][ny] = nc;
            queue.push([nx, ny, dir, nc]);
        }
    }
}

또 하나의 개선점은 Greedy한 접근방식을 사용하는 것 입니다. 최종적으로 알고 싶은 결과가 가장 작은 노력이 드는 경로이기에 그때 그때 순간에서의 최선의 선택을 수행 및 누적시켜 결과적으로 원하는 답을 찾는 방식입니다. 최단거리 문제에 유효한 다익스트라 알고리즘의 동작 방식을 흉내낸 것이라 생각하면 됩니다.

 

이전까지는 BFS탐색을 하면서 목적지에 도착하는 경로를 찾았더라도 해당 노력 값이 최소 노력임이 보장되지 않아 모든 탐색이 끝날때까지 기다려야 했습니다. 하지만 Greedy한 방식을 적용한다면 queue에서 선택된 값이 목적지라면 이 때의 노력 값은 최소 값임이 보장됩니다.

const efforts = new Array(rows).fill(0).map(val => new Array(cols).fill(Infinity));
effort[0][0] = 0;

const queue = [[0, 0, -1, 0]]
const move = [[-1, 0], [0, 1], [1, 0], [0, -1]];
while (queue.length) {
    const [cx, cy, cd, ce] = queue.pop();
    
    if (cy == rows-1 && cy == cols-1) return ce;
    
    for (let dir = 0; dir < 4; i++) {
        if (cd != -1 && cd == (dir+2)%4) { continue; }

          const nx = cx + move[i][0],
              ny = cy + move[i][1];
        if (nx < 0 || nx >= rows || ny < 0 || ny >= cols) { continue; }

        const nc = Math.max(Math.abs(heights[nx] - heights[ny), ce);
        if (efforts[nx][ny] > nc) {
            efforts[nx][ny] = nc;
            queue.push([nx, ny, dir, nc]);
            // 큐에 삽입한 후, 정렬을 통해 노력이 가장 작은 좌표가 배열의 끝에 위치하도록 함
            queue.sort((a, b) => b[3] - a[3]);
        }
    }
}

※ 위 자바스크립트 코드에서는 배열에 내장되어있는 sort() 함수를 사용하였는데, 이보다는 별도의 최소힙을 구현하는 것이 더 빠름(Python의 경우, 자체적으로 heapq모듈이 있으니 이것을 사용해서 문제 풀이 가능)

 

두 번째 방식인, Binary Search + DFS는 LeetCode의 힌트를 보고 알게 된 방법으로 동작 방식에 대해서만 간략히 서술하도록 하겠습니다.

 

우선 이진탐색 대상은 찾고자 하는 노력입니다. 탐색 범위는 0 ~ 10⁶ 또는 0 ~ heights의 최대값입니다. 탐색 범위의 감소는 DFS의 결과물을 기준으로 수행됩니다. DFS는 mid = low + ((high - low) / 2)를 넘지 않는 경로가 존재하는지 찾아 그 결과를 반환합니다. 만약 경로가 존재한다면 더 적은 노력의 경로가 존재하는지 찾기 위해 high = mid로 수정하고, 존재하지 않으면 low = mid + 1로 조절하는 것입니다.

 

아래는 Binary Search + DFS을 이용해 작성한 코드입니다.

var minimumEffortPath = function(heights) {
    const row = heights.length,
          col = heights[0].length;
    let visited = [];
	
    // DFS 방식으로 경로 찾기
    function dfs(x, y, k) {
        visited[x][y] = true;

        for (let [i, j] of [[-1, 0], [0, 1], [1, 0], [0, -1]]) {
            const n_x = x + i,
                  n_y = y + j;

            if (n_x < 0 || n_x >= row || n_y < 0 || n_y >= col || visited[n_x][n_y]) { continue; }

            if (k >= Math.abs(heights[n_x][n_y]-heights[x][y])) { dfs(n_x, n_y, k); }
        }
    }
	
    // 이진 탐색
    let l = 0, r = 1000000;
    while (l < r) {
        const mid = l + Math.floor((r - l) / 2);
        visited = new Array(row).fill(0).map(val => new Array(col).fill(false));

        dfs(0, 0, mid)
        if (visited[row-1][col-1]) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }

    return l;
};

Github : 1631.js

opwe37/Algorithm-Study